Evangelista Torricelli

Evangelista Torricelli se narodil 15. října 1608 ve městě Faenza v Itálii. Jeho rodiče nebyli bohatí – otec byl tkalec a rodina žila skromně. Po jeho smrti se o mladého Evangelistu postaral strýc, mnich z benediktinského řádu, který rozpoznal chlapcův mimořádný talent pro matematiku.

Díky tomu mohl Torricelli studovat u jezuitů a později i u slavného matematika Benedetta Castelliho, žáka samotného Galilea Galileiho. Právě Castelli svého nadaného studenta doporučil stárnoucímu Galileovi – a tak se Torricelli stal jeho asistentem. Po Galileově smrti v roce 1642 převzal jeho místo dvorního matematika u rodu Medicejských ve Florencii. Tam také zůstal až do své předčasné smrti 25.10. 1647, kdy mu bylo pouhých 39 let.

Experiment, který změnil pohled na svět

Torricelliho jméno se navždy zapsalo do dějin vědy díky jednomu jednoduchému, ale převratnému experimentu. Naplnil skleněnou trubici rtutí, uzavřel ji, obrátil a ponořil do nádoby se stejnou kapalinou. Všiml si, že část rtuti v trubici zůstala a nad ní vznikl prázdný prostor. Lidé tehdy věřili, že „příroda nesnáší prázdno“ – tedy že vakuum neexistuje. Torricelli však ukázal, že výšku rtuťového sloupce drží tlak vzduchu. Vzduch tedy musí něco vážit! A prostor nad rtutí je opravdu prázdný – vakuum.

Z tohoto experimentu vznikl rtuťový barometr – přístroj, který dodnes používáme k měření atmosférického tlaku. Na jeho počest se později jednotka tlaku pojmenovala torr (1 torr = 1/760 atmosféry).

Když nekonečno dává smysl

Torricelli se ale neproslavil jen jako fyzik. Patřil také mezi první, kteří začali uvažovat o nekonečnu v matematice. Zkoumal křivky, plochy a objemy pomocí tehdy nové metody zvané indivizibila – jakéhosi předchůdce infinitesimálního počtu.

Jeho nejslavnějším matematickým „paradoxem“ je tzv. Torricelliho trouba (nebo také Gabrielův roh): těleso, které má konečný objem, ale nekonečně velký povrch. Představte si nádobu, kterou byste mohli naplnit, ale nikdy byste ji neumyli, protože je její povrch nekonečný! Tento paradox vyvolal mezi učenci vášnivé debaty o tom, co vlastně znamená „nekonečno“.

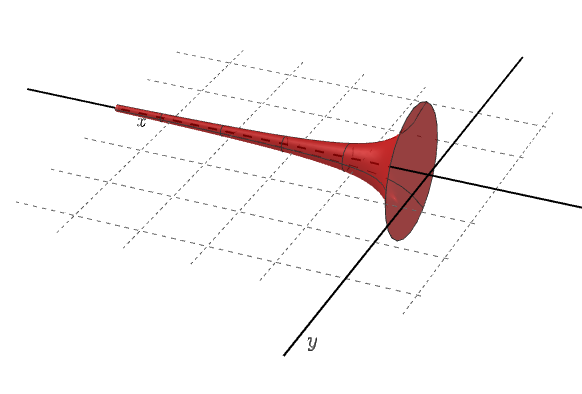
Torricelliho věta: když kapalina padá

Kromě barometru stojí za zmínku i tzv. Torricelliho věta z mechaniky kapalin. Ta říká, že rychlost, s jakou kapalina vytéká z otvoru nádoby, je stejná jako rychlost, jakou by těleso získalo volným pádem z výšky hladiny nad otvorem. Matematicky to vyjádřil vztahem:

I tento jednoduchý vztah je dnes základem mnoha výpočtů v hydrodynamice.

Inspirace pro Pascala

O Torricelliho práci se dozvěděl v roce 1646 prostřednictvím inženýra Pierra Petita matematik a fyzik Blaise Pascal. Pascal se rozhodl ověřit Torricelliho závěry a v roce 1648 provedl experiment, při němž nechal svého švagra Florina Périer vynést barometr na vrchol hory Puy de Dôme. Naměřený pokles hladiny rtuti potvrdil, že atmosférický tlak klesá s nadmořskou výškou, čímž Pascal potvrdil Torricelliho hypotézu o váze vzduchu

Dědictví vědce s duší filozofa

Torricelli žil krátce, ale jeho odkaz přetrval staletí. Propojil matematiku a experiment, myšlenku a praxi. Ukázal, že svět kolem nás se dá měřit, zkoumat a popisovat čísly – a přitom zůstává plný tajemství.

Bez jeho experimentů by nebylo moderní meteorologie, fyziky kapalin ani diskusí o nekonečnu, které vedly až k Newtonovu a Leibnizovu počtu. Evangelista Torricelli byl mostem mezi Galileem a moderní vědou.

V Newtonově díle Philosophiæ Naturalis Principia Mathematica (1687) se nachází zmínky o Torricelliho zákonu, který popisuje rychlost výtoku kapaliny z nádoby. V druhém vydání Principií z roku 1713 Newton tento zákon podporuje, i když s jistými výhradami. V třetím vydání z roku 1726 se k němu vrací a znovu jej potvrzuje.

Potíže s prázdnotou

V 17. století byla církevní autorita v Evropě stále velmi silná a její vliv zasahoval i do vědeckého myšlení. Aristotelésova teorie „horror vacui“ (příroda nesnáší prázdnotu) byla hluboce zakořeněná v tehdejším světovém názoru. Tato teorie tvrdila, že prázdný prostor nemůže existovat, protože by byl v rozporu s přirozeným řádem světa. Církev tuto myšlenku přijala a podporovala, což vedlo k odmítání jakýchkoli pokusů o experimentální prokázání existence vakua.

Evangelista Torricelli, žák Galilea Galileiho, se však rozhodl tuto dogmatickou představu vyvrátit. V roce 1643 provedl experiment, při kterém napustil skleněnou trubici rtutí, uzavřel ji a obrátil. Když trubici ponořil do nádoby s rtutí, zjistil, že část rtuti v trubici klesla, čímž vznikl prostor nad rtutí. Tento prostor nazval „vakuum“, čímž popřel Aristotelovu teorii a ukázal, že prázdný prostor může existovat.

Tento objev měl dalekosáhlé důsledky. Torricelliho experiment ukázal, že vzduch má hmotnost a že tlak vzduchu může podporovat sloupec rtuti. Tímto způsobem přispěl k rozvoji moderní fyziky a k přehodnocení tehdejších vědeckých a filozofických dogmat.

Jaká byla Toricelliho matematika?

Torricelli pracoval v době, kdy kalkulus ještě nebyl formálně vyvinut (Newton a Leibniz jej popsali až ve 2. polovině 17. století). Přesto používal metody, které se dnes považují za předchůdce integrálního počtu, zejména tzv. metodu indivizibilů (method of indivisibles) od Bonaventury Cavalieriho.

Jak Torricelli pracoval s „nekonečnem“ a plochami

Metoda indivizibilů: Torricelli rozkládal plochy a objemy na nekonečně malé „řezové“ elementy, které byly v jeho představě „indivisibilní“. Například při výpočtu objemu Torricelliho trouby (Gabrielův roh) se sečítaly nekonečné, ale stále velmi malé „řezné“ plochy.

Paradox nekonečna: Aby ukázal, že těleso může mít nekonečný povrch a konečný objem, potřeboval pracovat s nekonečnými řadami či součty velmi malých elementů — v principu jde o integraci. Formálně ale ještě integroval „geometricky“, nikoli algebraicky jako v Newtonově nebo Leibnizově kalkulu.

Inspirace od Cavalieriho: Torricelli převzal ideu, že plocha je složena z nekonečně mnoha linek a objem z nekonečně mnoha plošek. To mu umožnilo pracovat s nekonečně malými veličinami a řešit problémy, které vypadaly paradoxně.

Obešel se tak bez formálních integrálů, ale jeho myšlení a výpočty byly přímým předchůdcem integrálního počtu. Díky jeho geometrickému přístupu k nekonečnu mohl řešit problémy, které by se bez infinitesimálních metod řešily velmi obtížně.